祖源計算器中的Fst分布密度之統計學意義初探
繼一下這兩篇文章:
http://www.sofreetech.com/question/25090
http://www.sofreetech.com/question/25246
我們對祖源計算器中的Fst分布密度使用matlab的分布擬合器進行了統計學上的分析以發現分布密度函數(PDF)
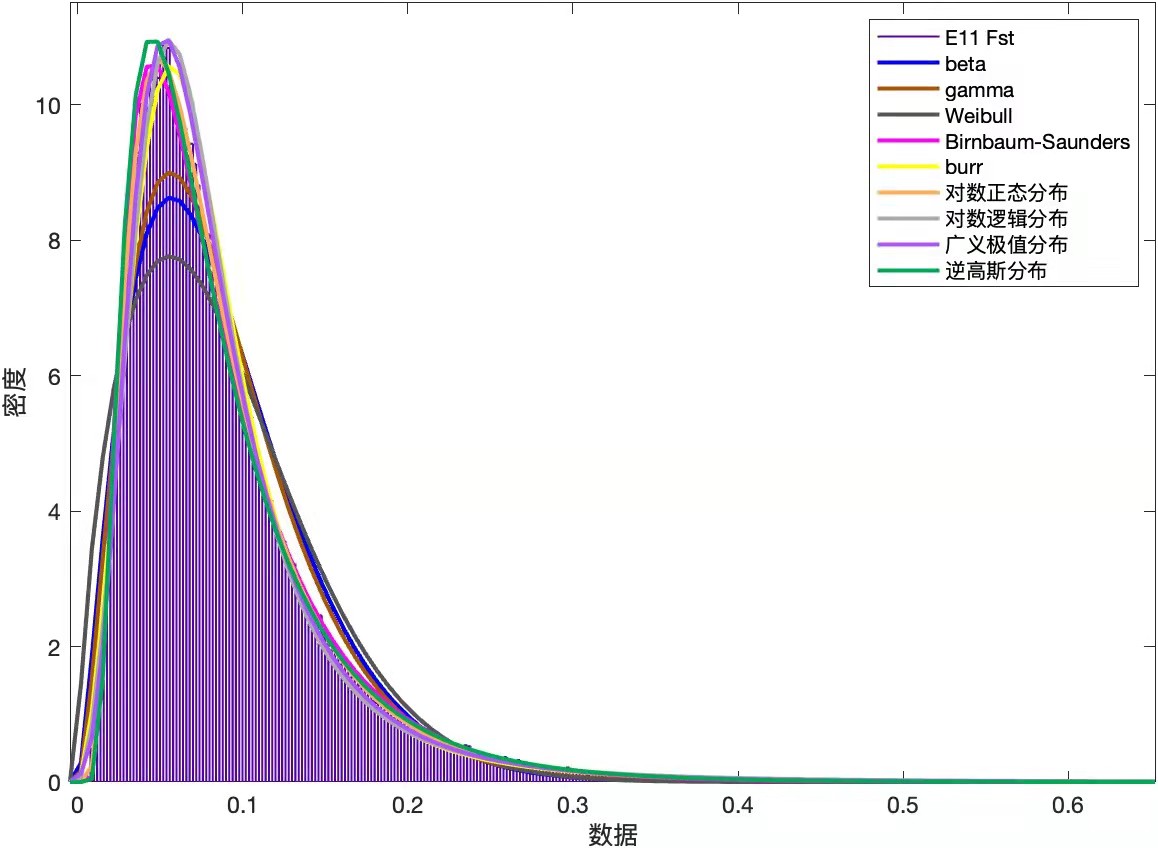
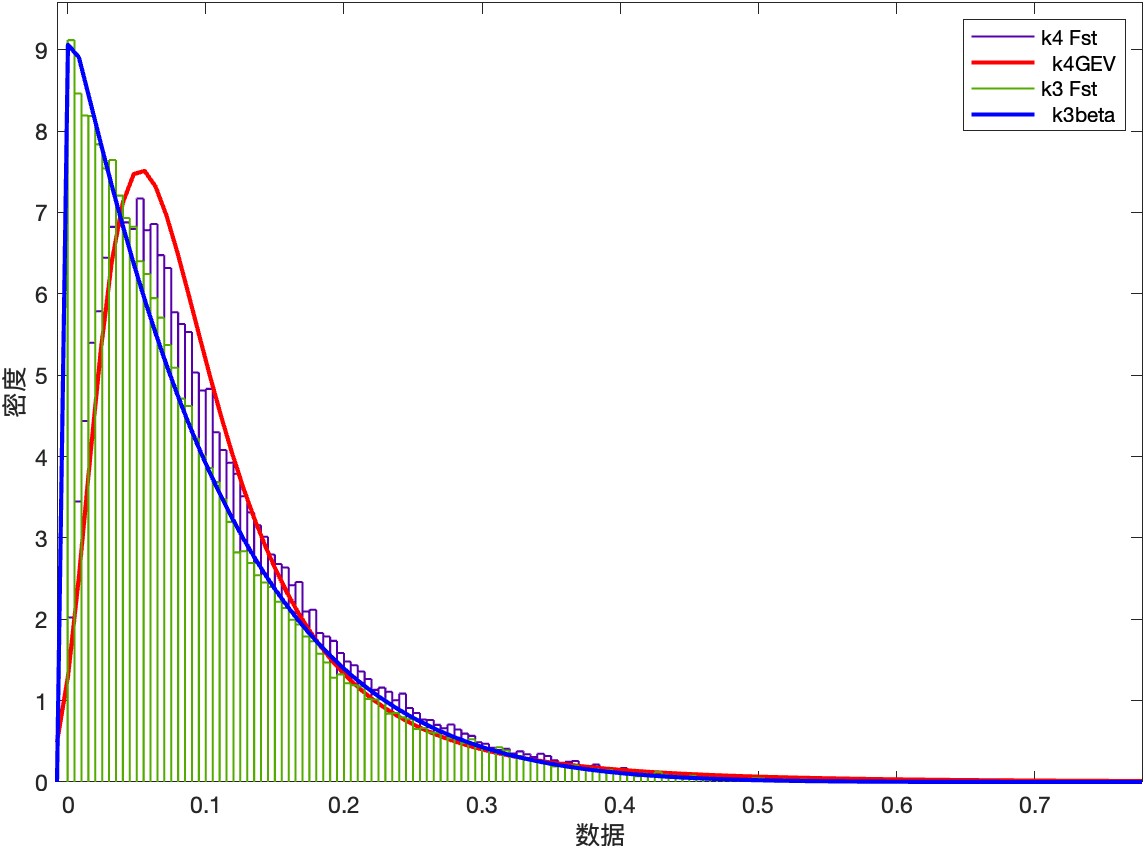
首先以e11為入手點篩選出來哪些分布函數能比較好的擬合e11這個計算器。效果如圖一(過于離譜的結果已經被排除了)
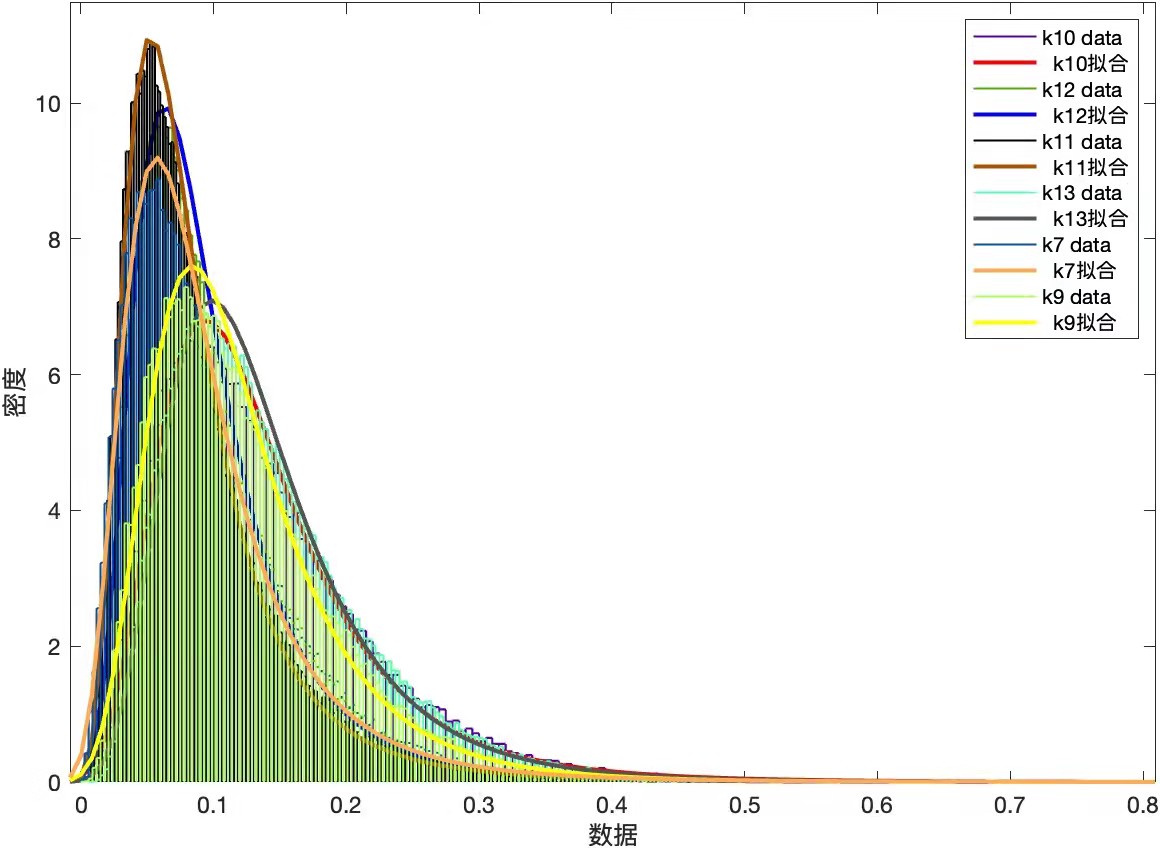
之后,分別用篩選出來的幾個分布函數擬合其他k值的計算器,篩選出可以在不同k值下都能(或大部分)比較好擬合的分布函數。效果如圖二(其他不符合的均被排除,圖中所顯示的是廣義極值分布)
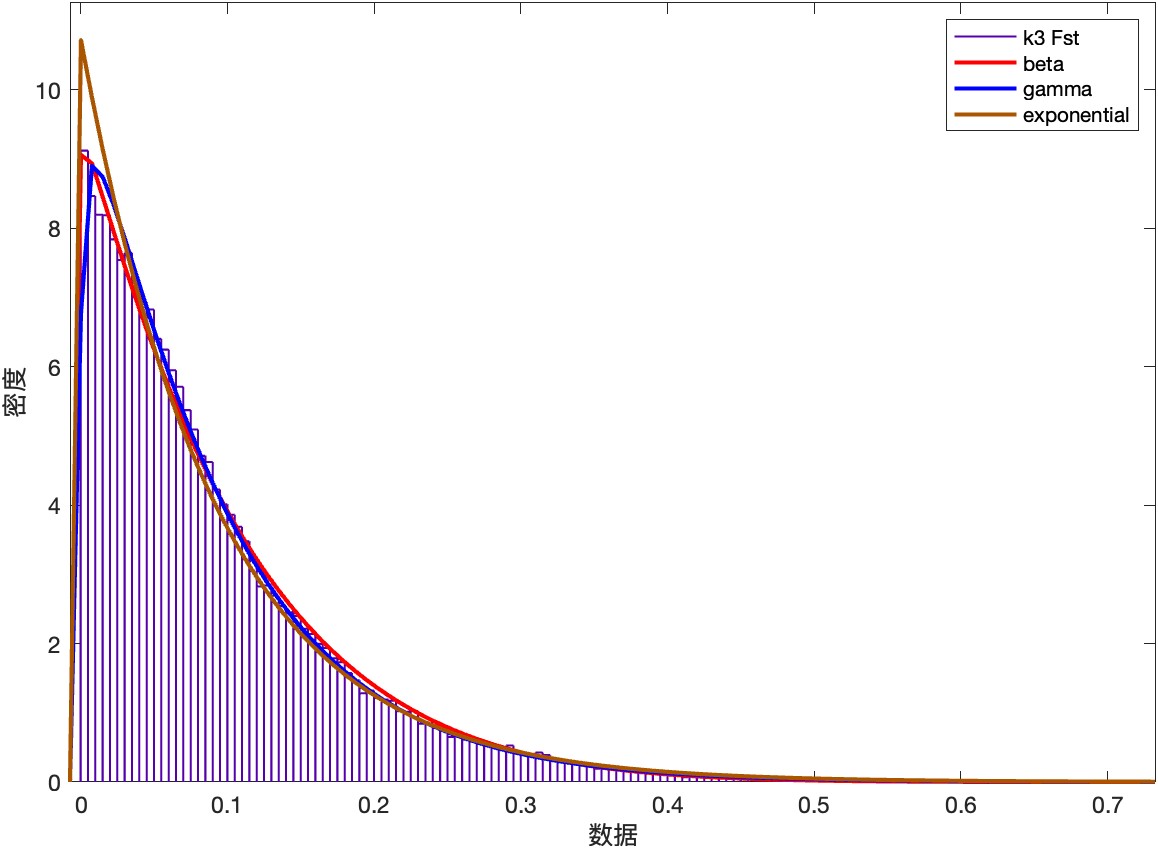
接著,我們將三個梯度k值(以k取3,12和47為例)發現低k值組還是不能很好的擬合。于是我們再用其他的分布密度函數對小k值的Fst分布密度進行擬合,進行篩選,發現在k值為3時,beta函數能較好的擬合。如下圖所示:
最后,我們簡單的對擬合出的系數進行分析。我們首先觀察到廣義極值函數中有系數k是否為0的兩種情況。如下圖所示:
而通過擬合,無論在何計算器k值時,廣義極值函數的系數k均不為0,所以我們抹去廣義極值函數中系數k為0的情況以簡化函數。并且由k值為3向上遞增觀察密度函數形狀,發現當k值為4時密度函數變為廣義極值函數形狀。所以確定確定了兩函數的使用條件。合并并簡化后得到如下圖所示的經驗公式:
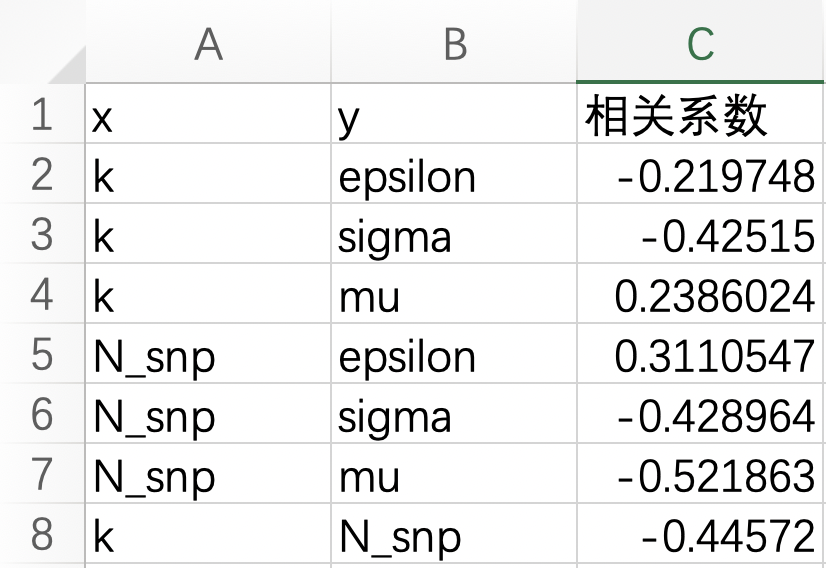
另外,通過計算自變量與因變量間的相關系數(如下表),我們確定k與系數sigma和mu以及計算器snp數與sigma和mu之間均呈負相關,并且通過計算相關系數的絕對值并比較大小以及k與snp數程負相關(因為兩量間相關系數也為負)可知,很有可能是k值首先影響計算器snp數,再間接影響兩系數的。當然這里都是猜測,具體還需要進一步研究才能確定。
?
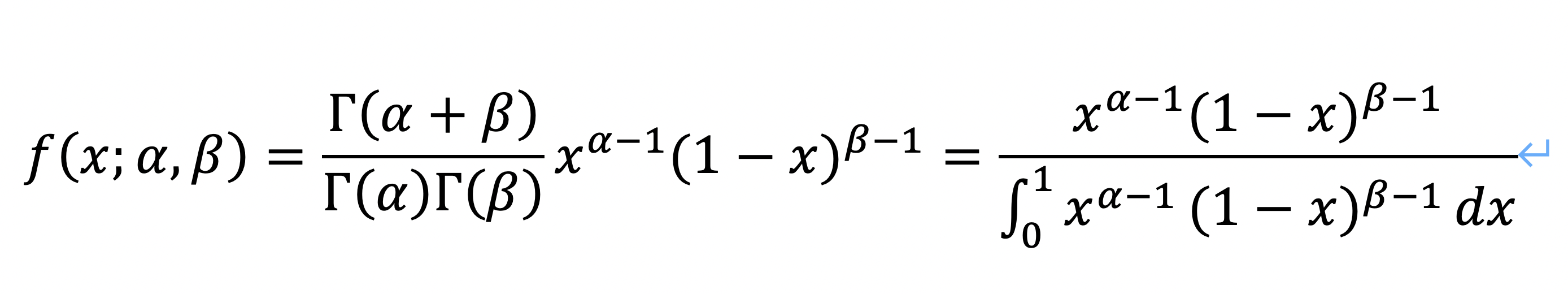
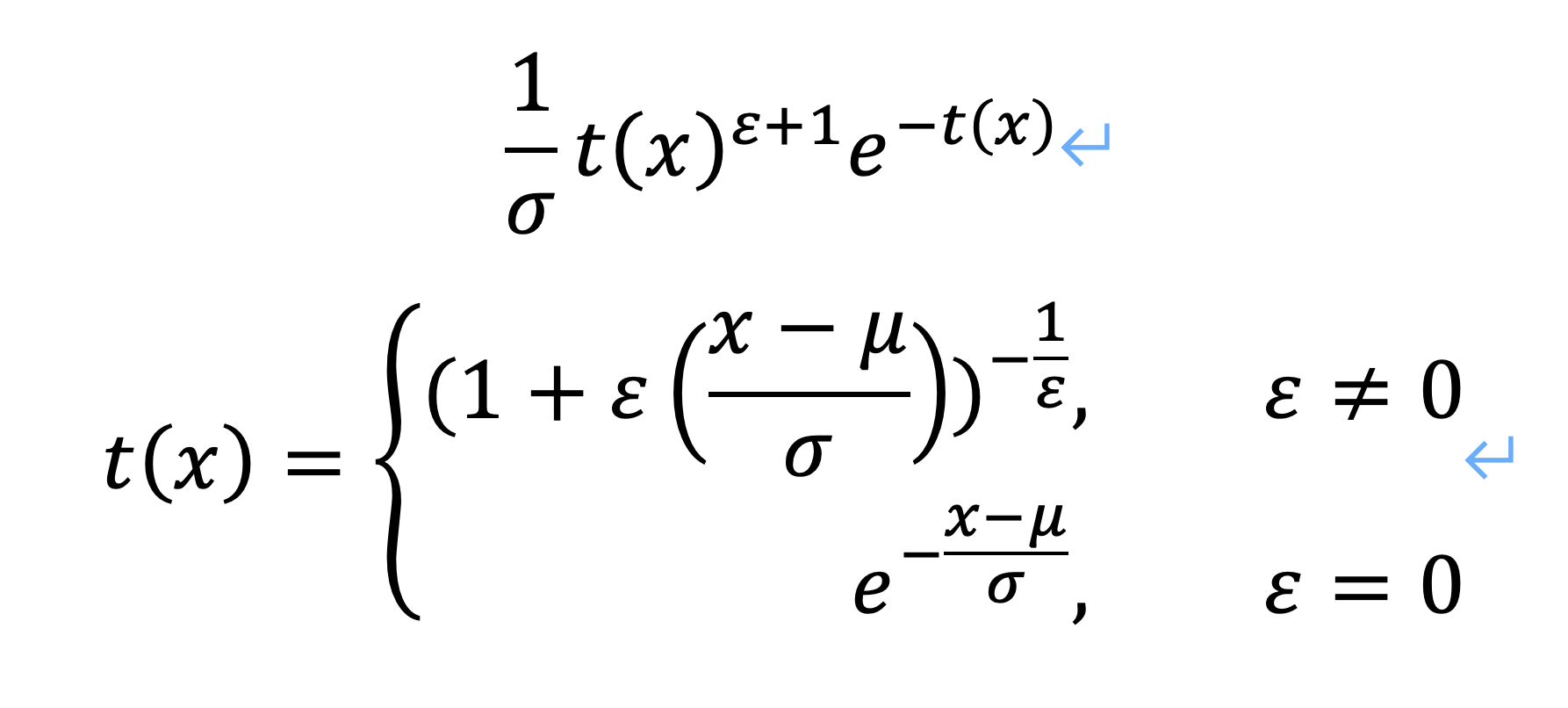
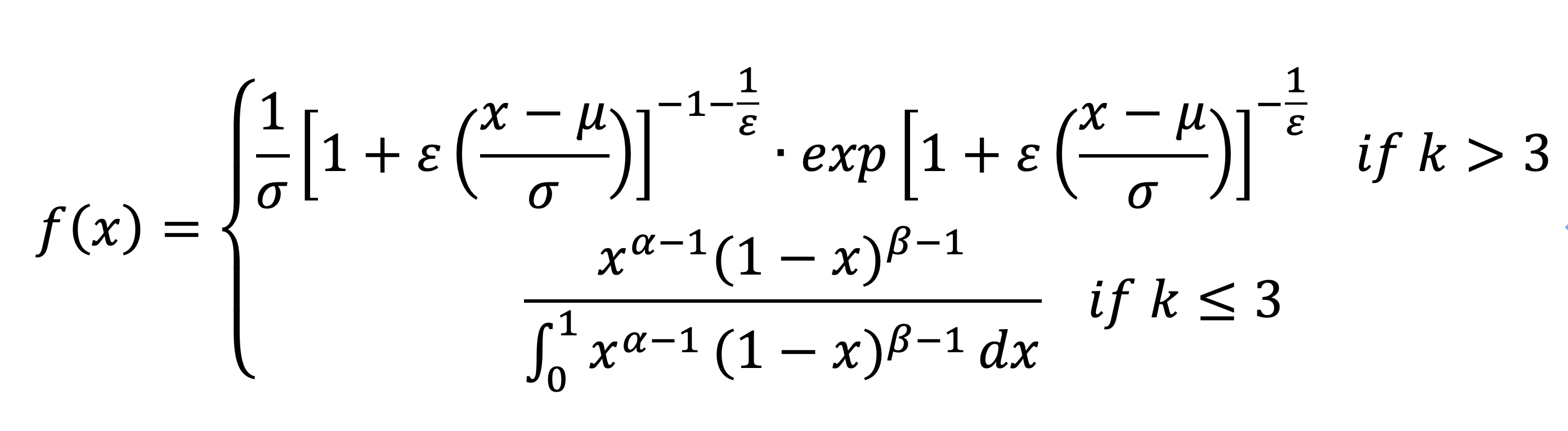


2 個回復
贊同來自:
贊同來自:
要回復問題請先登錄或注冊